Merkle Tree & Merkle Root Explained
In the intricate world of cryptography and blockchain technology, understanding the foundational concepts is crucial. Among these are the Merkle tree and the Merkle root, terms often used interchangeably by newcomers but representing distinct ideas. While both play a pivotal role in ensuring data integrity and consistency in various cryptographic applications, they serve different functions within the system.
This blog post will delve into the nuances between the Merkle tree and the Merkle root, offering clarity on their roles and significance in the blockchain ecosystem.
What is a Merkle tree?
A Merkle tree, or binary hash tree, involves taking large amounts data and making it more manageable to process. In the case of blockchain technology, merkle trees are used to organize regular transactions such as: “Alice sent Bob 5 Bitcoins”, in a way that utilizes fewer resources.
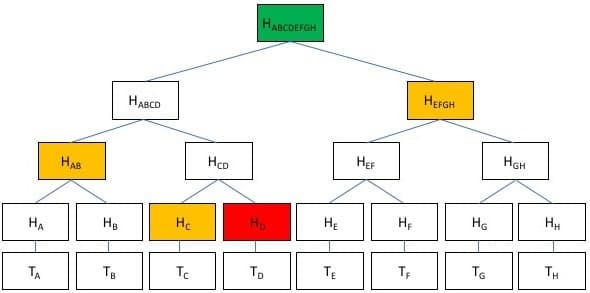
Source: Investopedia
“TA” represents a normal transaction, like the one described above. These transactions are hashed individually to give their corresponding hash value. For example, “TD” is put through a hash function to give its corresponding hash value of “HD“. In the case of Bitcoin, the hash function it uses is the SHA-256 hash function. If you are unsure of what a hash function is, then I suggest that you read my previous article on what the SHA-256 function is, and how it relates to Bitcoin.
After each transaction has been individually hashed to produce its corresponding hash value, the new hash values are combined with an adjacent partner to be hashed once again. For example, the hash values “HC” and “HD” are combined and hashed to produce the hash “HCD“. In the above example, there are 8 transactions with their own corresponding hash values. However, if there had been an odd number of hash values, such as 7, then the 7th hash is simply paired with itself and hashed to produce a new hash value. That is, “HH” and “HH” would be combined to give “HHH“.
This process is repeated until the last hash value is obtained. This value is known as the merkle root.
What is a Merkle root?
In the above example, the merkle root is labelled “HABCDEFGH“. The merkle root is 32 bytes in size and is then taken to be placed inside the block header; it represents a summary of all transaction data.
Why a Merkle tree is important
Advantages of a merkle tree structure include:
- Easy to check if transactions have been tampered with
- Uses fewer resources
- Easy to verify if a specific transaction has been added to the block
Tamper proof: One benefit of organising transactions in a merkle tree structure is, it becomes straightforward to verify that no transaction in a block has been tampered with. If for example the transaction: “TH” were to be changed “TXYZ”, the corresponding hash value would be different. Therefore, when the resulting hash is combined with its adjacent hash partner, the ensuring hash would be different. This leads to a completely different merkle root, and therefore, it can concluded that if the merkle root were ever to change, one or more transactions must have been tampered with.
Uses fewer resources: Organizing transactions in a merkle tree structure uses fewer resources than hashing transactions in one bundle and inserting that into the block header. Even though technically a cryptocurrency such as Bitcoin would still be able to function if all transactions were to be organized in this way, it would still use up too many resources. This method of handling transactions may result in fewer nodes on the Bitcoin network due to the higher costs of handling extra resources. Therefore, leading to a less decentralized Bitcoin network.
Verifying a transaction: A merkle tree allows for a user to check that a specific transaction has been included in a block without having to download the entire blockchain. Through the use of lightweight clients such as, Simplified Payment Verification (SPV) protocols, users can query the blockchain to check that their transaction has been included.
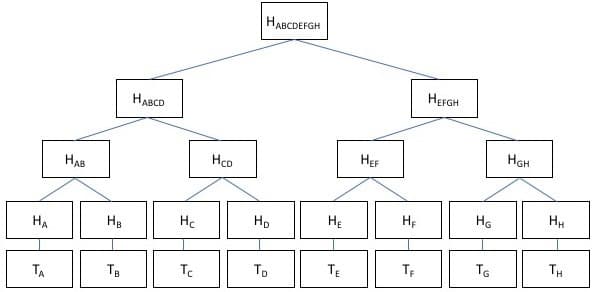
Source: Investopedia
For example, if as user wanted to check the transaction “HD” had been included in a block, instead of downloading the whole blockchain and checking, the only values the user would need are: The merkle root, “HEFGH”, “HAB” and “HC”. Even though information is still needed to verify that a transaction has been included in the block, it is still significantly better than downloading the whole blockchain to check.
Conclusion
Merkle trees are a powerful method in organising transactions to allow for cryptocurrencies such as Bitcoin and Ethereum to function as they do. Without merkle trees, it is fair to argue that the cryptocurrencies that we know today may have been forced to operate in a much less efficient way.